The Pythagorean Theorem is one of the most celebrated mathematical theorem in the world. According Guinness Book World of Records, it boasts more than 500 proofs. Most famous of the proof is the proof provided by Euclid in Elements
Many mathematicians from antiquity to modern times had marveled at this rule and proved it in different ways. Here we will see how Bhaskara, one of the most important mathematicians of old India proved it geometrically.
The theorem says a2 + b2 = c2 : where a and b are sides of a right triangle and c is its hypotenuse
Bhaskara gives the following diagram to prove the theorem:
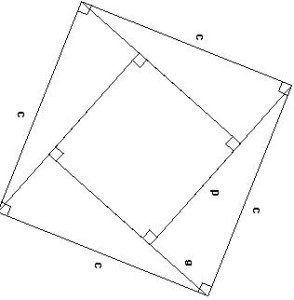
Bhaskara’s description of Pythagoras Theorem
From the picture, you can see that
Area Large squire is = Area of all 4 triangles + area of smaller squire
c * c = 4 * ( 1/2 ) a * b + (b-a) * (b-a) = 2ab – ( a2 + b2 + 2ab)
c2 = a2 + b2
which is the Pythagorean theorem
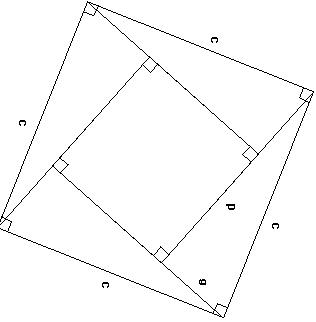
Area Large squire is = Area of all 4 triangles + area of smaller squire
c * c = 4 * ( 1/2 ) a * b + (b-a) * (b-a) = 2ab + a2 + b2 – 2ab = a2 + b2
c2 = a2 + b2
which is the Pythagorean theorem